Subsampling under logistic regression for a potentially misspecified model

Using this function sample from big data under logistic regression for a potentially misspecified model. Subsampling probabilities are obtained based on the A-, L- and L1- optimality criteria with the RLmAMSE (Reduction of Loss by minimizing the Average Mean Squared Error).

Usage

modelMissLogSub(r0,rf,Y,X,N,Alpha,proportion,model="Auto")

Arguments

r0: sample size for initial random sample
rf: final sample size including initial(r0) and optimal(r) samples
Y: response data or Y
X: covariate data or X matrix that has all the covariates (first column is for the intercept)
N: size of the big data
Alpha: scaling factor when using Log Odds or Power functions to magnify the probabilities
proportion: a proportion of the big data is used to help estimate AMSE values from the subsamples
model: formula for the model used in the GAM or the default choice

Value

The output of modelMissLogSub gives a list of

Beta_Estimates estimated model parameters after subsampling

Utility_Estimates estimated A-, L- and L1- optimality values for the obtained subsamples

AMSE_Estimates matrix of estimated AMSE values after subsampling

Sample_A-Optimality list of indexes for the initial and optimal samples obtained based on A-Optimality criteria

Sample_L-Optimality list of indexes for the initial and optimal samples obtained based on L-Optimality criteria

Sample_L1-Optimality list of indexes for the initial and optimal samples obtained based on L1-Optimality criteria

Sample_RLmAMSE list of indexes for the optimal samples obtained based on RLmAMSE

Sample_RLmAMSE_Log_Odds list of indexes for the optimal samples obtained based on RLmAMSE with Log Odds function

Sample_RLmAMSE_Power list of indexes for the optimal samples obtained based on RLmAMSE with Power function

Subsampling_Probability matrix of calculated subsampling probabilities

Details

The article for this function is in preparation for publication. Please be patient.

Two stage subsampling algorithm for big data under logistic regression for potential model misspecification.

First stage is to obtain a random sample of size \(r_0\) and estimate the model parameters. Using the estimated parameters subsampling probabilities are evaluated for A-, L-, L1-optimality criteria, RLmAMSE and enhanced RLmAMSE(log-odds and power) subsampling methods.

Through the estimated subsampling probabilities a sample of size \(r \ge r_0\) is obtained. Finally, the two samples are combined and the model parameters are estimated for A-, L-, L1-optimality, RLmAMSE and enhanced RLmAMSE (log-odds and power).

NOTE : If input parameters are not in given domain conditions necessary error messages will be provided to go further.

If \(r \ge r_0\) is not satisfied then an error message will be produced.

If the big data \(X,Y\) has any missing values then an error message will be produced.

The big data size \(N\) is compared with the sizes of \(X,Y\),F_estimate_Full and if they are not aligned an error message will be produced.

If \(\alpha > 1\) for the scaling vector is not satisfied an error message will be produced.

If proportion is not in the region of \((0,1]\) an error message will be produced.

model is a formula input formed based on the covariates through the spline terms (s()), squared term (I()), interaction terms (lo()) or automatically. If model is empty or NA or NAN or not one of the defined inputs an error message is printed. As a default we have set model="Auto", which is the main effects model wit the spline terms.

References

Adewale AJ, Wiens DP (2009). “Robust designs for misspecified logistic models.” Journal of Statistical Planning and Inference, 139(1), 3--15. Adewale AJ, Xu X (2010). “Robust designs for generalized linear models with possible overdispersion and misspecified link functions.” Computational statistics & data analysis, 54(4), 875--890.

Examples

Beta<-c(-1,0.75,0.75,1); family <- "logistic"; N<-10000
X_1 <- replicate(2,stats::runif(n=N,min = -1,max = 1))

Temp<-Rfast::rowprods(X_1)
Misspecification <- (Temp-mean(Temp))/sqrt(mean(Temp^2)-mean(Temp)^2)
X_Data <- cbind(X0=1,X_1);
Full_Data<-GenModelMissGLMdata(N,X_Data,Misspecification,Beta,Var_Epsilon=NULL,family)

r0<-300; rf<-rep(100*c(6,9),50);
Original_Data<-Full_Data$Complete_Data[,-ncol(Full_Data$Complete_Data)];

# cl <- parallel::makeCluster(4)
# doParallel::registerDoParallel(cl)
if (FALSE) {
Results<-modelMissLogSub(r0 = r0, rf = rf,
                         Y = as.matrix(Original_Data[,1]),
                         X = as.matrix(Original_Data[,-1]),
                         N = N, Alpha = 10, proportion = 0.3)

# parallel::stopCluster(cl)

plot_Beta(Results)
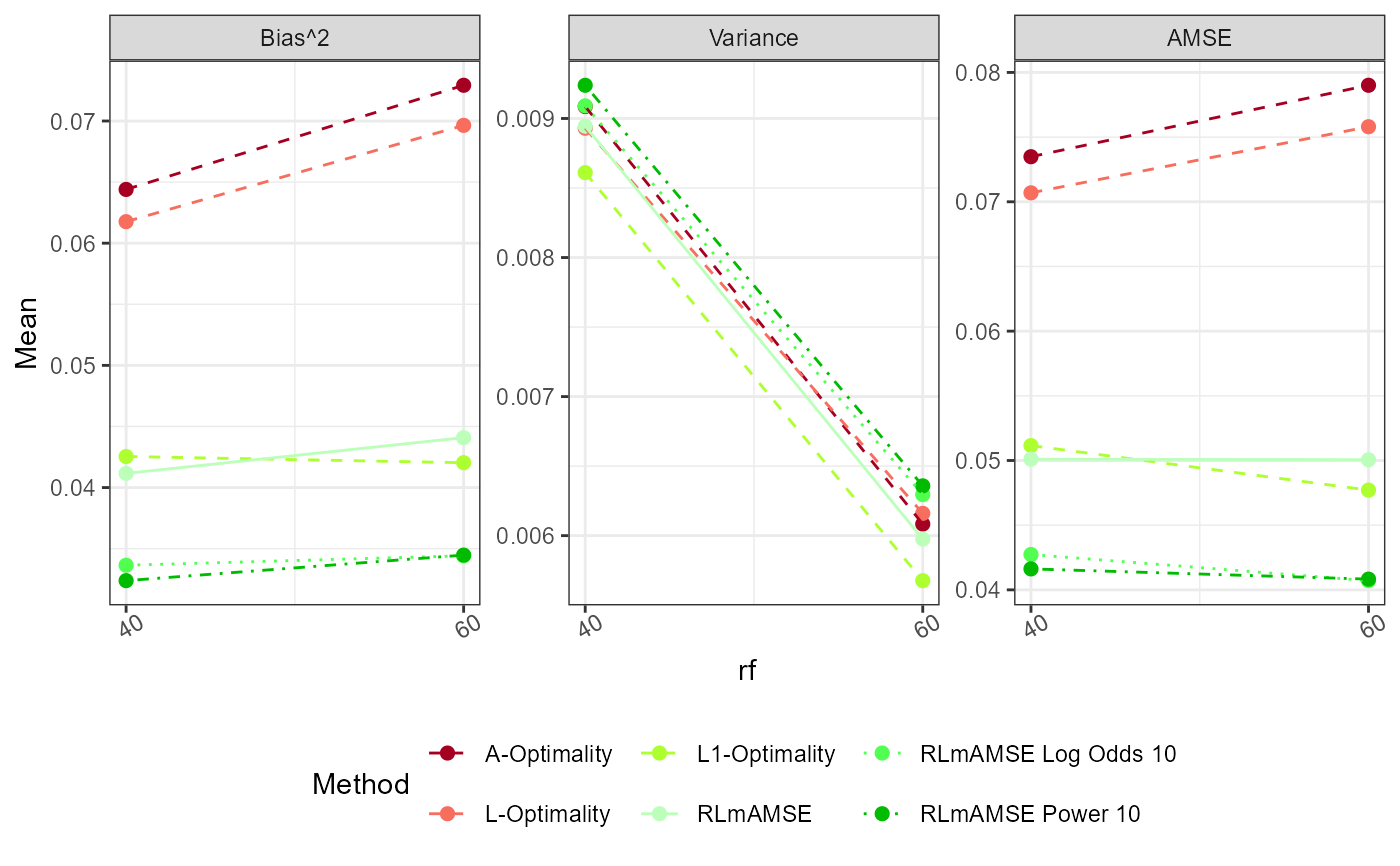
plot_AMSE(Results)
}