
Poisson Regression : Model robust and misspecification
Source:vignettes/Poisson_Regression.Rmd
Poisson_Regression.Rmd
# Load the R packages
library(NeEDS4BigData)
library(ggplot2)
library(ggpubr)
library(kableExtra)
library(tidyr)
library(psych)
library(gam)
# Theme for plots
Theme_special<-function(){
theme(legend.key.width= unit(1,"cm"),
axis.text.x= element_text(color= "black", size= 12, angle= 30, hjust=0.75),
axis.text.y= element_text(color= "black", size= 12),
strip.text= element_text(colour= "black", size= 12, face= "bold"),
panel.grid.minor.x= element_blank(),
axis.title= element_text(color= "black", face= "bold", size= 12),
legend.text= element_text(color= "black", size= 11),
legend.position= "bottom",
legend.margin= margin(0,0,0,0),
legend.box.margin= margin(-1,-2,-1,-2))
}Understanding the bike sharing data
Fanaee-T and Gama (2013) collected data to understand the bike sharing demands under the rental and return process. The data contains \(4\) columns and has \(17,379\) observations, first column is the response variable and the rest are covariates. We consider the covariates a) temperature (\(x_1\)), b) humidity (\(x_2\)) and c) windspeed (\(x_3\)) to model the response, the number of bikes rented hourly. The covariates are scaled to be mean of zero and variance of one.
Given data is analysed under two different scenarios,
- model robust or average subsampling methods assuming that a set of models can describe the data.
- sampling method assuming the main effects model is potentially misspecified.
# Selecting 100% of the big data and prepare it
Original_Data<-cbind(Bike_sharing[,1],1,Bike_sharing[,-1])
colnames(Original_Data)<-c("Y",paste0("X",0:ncol(Original_Data[,-c(1,2)])))
# Scaling the covariate data
for (j in 3:5) {
Original_Data[,j]<-scale(Original_Data[,j])
}
head(Original_Data) %>%
kable(format = "html",
caption = "First few observations of the bike sharing data.")| Y | X0 | X1 | X2 | X3 |
|---|---|---|---|---|
| 16 | 1 | -1.334609 | 0.9473452 | -1.553844 |
| 40 | 1 | -1.438475 | 0.8955129 | -1.553844 |
| 32 | 1 | -1.438475 | 0.8955129 | -1.553844 |
| 13 | 1 | -1.334609 | 0.6363514 | -1.553844 |
| 1 | 1 | -1.334609 | 0.6363514 | -1.553844 |
| 1 | 1 | -1.334609 | 0.6363514 | -0.821460 |
# Setting the sample sizes
N<-nrow(Original_Data); M<-250; k<-seq(6,18,by=3)*100; rep_k<-rep(k,each=M)Model robust or average subsampling
The method \(A\)- and \(L\)-optimality of model robust or average subsampling (Mahendran, Thompson, and McGree 2023) is compared against the \(A\)- and \(L\)-optimality subsampling (Ai et al. 2021; Yao and Wang 2021) method. Here five different models are considered 1) main effects model (\(\beta_0+\beta_1X_1+\beta_2X_2+\beta_3X_3\)), 2-4) main effects model with the squared term of each covariate (\(X^2_1 / X^2_2 / X^2_3\)) and 5) main effects model with all the squared terms (\(\beta_0+\beta_1X_1+\beta_2X_2+\beta_3X_3+\beta_4X^2_1+\beta_5X^2_2+\beta_6X^2_3\)). For each model \(j\) the mean squared error of the model parameters \(MSE_l(\tilde{\beta}_k,\hat{\beta})=\frac{1}{MJ} \sum_{i=1}^M \sum_{j=1}^J (\tilde{\beta}_{k,j} - \hat{\beta}_j)^2\) are calculated for the \(M=100\) simulations across the sample sizes \(k=(600,\ldots,1500)\) and the initial sample size is \(r1=300\). Here, for the \(l\)-th model \(\tilde{\beta}_k\) is the estimated model parameters from the sample of size \(k\) and \(\hat{\beta}\) is the estimated model parameters from the full big data, while \(j\) is index of the model parameter.
# Define the subsampling methods and their respective colours, shapes and line types
Method_Names<-c("A-Optimality","L-Optimality","A-Optimality MR","L-Optimality MR")
Method_Colour<-c("red","darkred","green","springgreen4")
Method_Shape_Types<-c(rep(8,2),rep(4,2))
Method_Line_Types<-c(rep("twodash",2),rep("dotted",2))
# Preparing the data for the model average method with squared terms
No_of_Variables<-ncol(Original_Data[,-c(1,2)])
Squared_Terms<-paste0("X",1:No_of_Variables,"^2")
term_no <- 2
All_Models <- list(c("X0",paste0("X",1:No_of_Variables)))
Original_Data_ModelRobust<-cbind(Original_Data,Original_Data[,-c(1,2)]^2)
colnames(Original_Data_ModelRobust)<-c("Y","X0",paste0("X",1:No_of_Variables),
paste0("X",1:No_of_Variables,"^2"))
for (i in 1:No_of_Variables)
{
x <- as.vector(combn(Squared_Terms,i,simplify = FALSE))
for(j in 1:length(x))
{
All_Models[[term_no]] <- c("X0",paste0("X",1:No_of_Variables),x[[j]])
term_no <- term_no+1
}
}
All_Models<-All_Models[-c(5:7)]
names(All_Models)<-paste0("Model_",1:length(All_Models))Apriori probabilities are equal
Consider for \(Q=5\) each model has an equal a priori probability (i.e \(\alpha_q=1/5,q=1,\ldots,5\)). Below is the code of implementation for this scenario.
All_Covariates<-colnames(Original_Data_ModelRobust)[-1]
# A- and L-optimality model robust subsampling for poisson regression
NeEDS4BigData::modelRobustPoiSub(r1=300,r2=rep_k,
Y=as.matrix(Original_Data_ModelRobust[,1]),
X=as.matrix(Original_Data_ModelRobust[,-1]),
N=N,Alpha=rep(1/length(All_Models),length(All_Models)),
All_Combinations = All_Models,
All_Covariates = All_Covariates)->Results## Step 1 of the algorithm completed.## Step 2 of the algorithm completed.
Final_Beta_modelRobust<-Results$Beta_Estimates
# Mean squared error and their respective plots for all five models
MSE_Beta_MR<-list(); plot_list_MR<-list()
for (i in 1:length(All_Models)) {
glm(Y~.-1,data=Original_Data_ModelRobust[,c("Y",All_Models[[i]])],
family="poisson")->All_Results
All_Beta<-coefficients(All_Results)
matrix(rep(All_Beta,by=nrow(Final_Beta_modelRobust[[i]])),
nrow = nrow(Final_Beta_modelRobust[[i]]),
ncol = ncol(Final_Beta_modelRobust[[i]][,-c(1,2)]),byrow = TRUE)->All_Beta
MSE_Beta_MR[[i]]<-data.frame("Method"=Final_Beta_modelRobust[[i]]$Method,
"Sample"=Final_Beta_modelRobust[[i]]$r2,
"MSE"=rowSums((All_Beta -
Final_Beta_modelRobust[[i]][,-c(1,2)])^2))
ggplot(MSE_Beta_MR[[i]] |> dplyr::group_by(Method,Sample) |>
dplyr::summarise(MSE=mean(MSE), .groups = 'drop'),
aes(x=factor(Sample),y=MSE,color=Method,group=Method,
linetype=Method,shape=Method))+
geom_point()+geom_line()+xlab("Sample size")+ylab("MSE")+
scale_color_manual(values = Method_Colour)+
scale_linetype_manual(values=Method_Line_Types)+
scale_shape_manual(values = Method_Shape_Types)+
theme_bw()+guides(colour = guide_legend(nrow = 2))+
Theme_special()->plot_list_MR[[i]]
}
ggarrange(plotlist = plot_list_MR,nrow = 3,ncol = 2,labels = "auto",
legend = "bottom",common.legend = TRUE)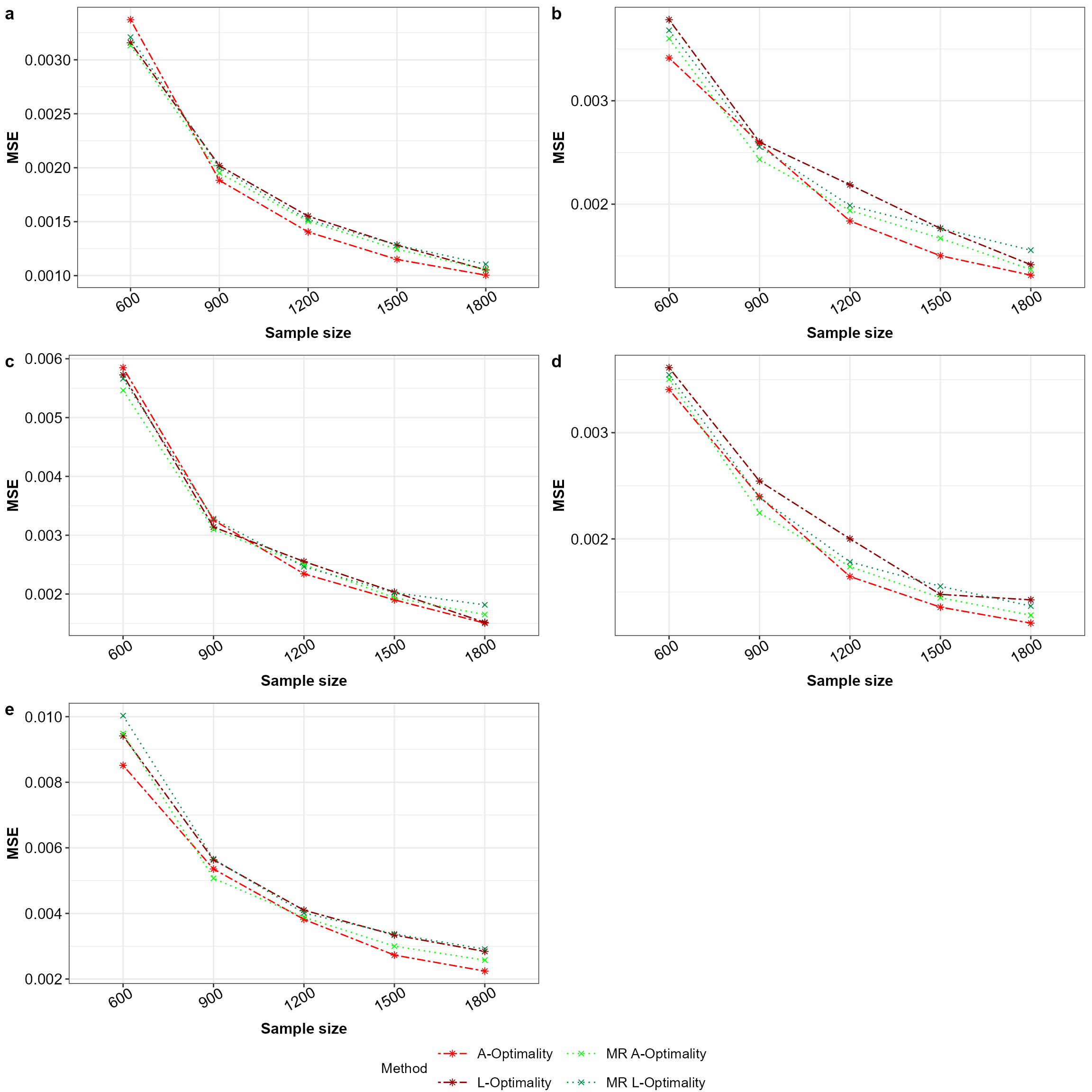
Mean squared error for all the models with equal apriori in the order a to e for Model 1 to 5 across the subsampling methods under comparison.
Main effects model is potentially misspecified
The final and third scenario is for comparison of the sampling method under the assumption that the main effects model is potentially misspecified against the \(A\)- and \(L\)-optimality subsampling method. Under the sampling method that accounts for potential model misspecification we take the scaling factor of \(\alpha=10\). As in scenario one an two the number of simulations and the sample sizes stay the same. We compare the mean squared error of the estimated model parameters, however as we assume the model is potentially misspecified the asymptotic approximation of the mean squared error from the predictions are calculated as well. Below is the code for this implementation.
# Define the sampling methods and their respective colors, shapes and line types
Method_Names<-c("A-Optimality","L-Optimality","RLmAMSE",
"RLmAMSE Log Odds 10","RLmAMSE Power 10")
Method_Colour<-c("red","darkred","yellowgreen","green","springgreen4")
Method_Shape_Types<-c(rep(8,2),rep(4,3))
Method_Line_Types<-c(rep("twodash",2),rep("dotted",3))
# For the big data fit the main effects model and estimate the contamination
interaction_terms <- combn(colnames(Original_Data[,-1])[-1],2,
FUN=function(x)paste(x,collapse="*"))
as.formula(paste("Y~",
paste(paste0("s(X",1:ncol(Original_Data[,-c(1,2)]),")"),
collapse="+"),"+",paste(paste0("s(",interaction_terms,")"),
collapse=" + ")))->my_formula
glm(Y~.-1,data=Original_Data,family="poisson")->Results
beta.prop<-coefficients(Results)
Xbeta_Final<-as.vector(as.matrix(Original_Data[,-1])%*%beta.prop)
fit_GAM<-gam::gam(formula = my_formula,data=Original_Data,family="poisson")
Xbeta_GAM<-gam::predict.Gam(fit_GAM,newdata = Original_Data[,-1])
f_estimate<-Xbeta_GAM - Xbeta_Final
# A- and L-optimality and RLmAMSE model misspecified sampling for poisson regression
NeEDS4BigData::modelMissPoiSub(r1=300,r2=rep_k,
Y=as.matrix(Original_Data[,1]),
X=as.matrix(Original_Data[,-1]),
N=N,Alpha=10, Beta_Estimate_Full = beta.prop,
F_Estimate_Full = f_estimate)->Results## Step 1 of the algorithm completed.## Step 2 of the algorithm completed.
Final_Beta_modelMiss<-Results$Beta_Estimates
Final_AMSE_modelMiss<-Results$AMSE_Estimates
matrix(rep(beta.prop,by=nrow(Final_Beta_modelMiss)),nrow = nrow(Final_Beta_modelMiss),
ncol = ncol(Final_Beta_modelMiss[,-c(1,2)]),byrow = TRUE)->All_Beta
# Plots for the mean squared error of the model parameter estimates
# and the AMSE for the main effects model
MSE_Beta_modelMiss<-data.frame("Method"=Final_Beta_modelMiss$Method,
"Sample"=Final_Beta_modelMiss$r2,
"MSE"=rowSums((All_Beta -
Final_Beta_modelMiss[,-c(1,2)])^2))
ggplot(MSE_Beta_modelMiss |> dplyr::group_by(Method,Sample) |>
dplyr::summarise(MSE=mean(MSE), .groups = 'drop'),
aes(x=factor(Sample),y=MSE,color=Method,group=Method,
linetype=Method,shape=Method))+
geom_point()+geom_line()+xlab("Sample size")+ylab("MSE")+
scale_color_manual(values = Method_Colour)+
scale_linetype_manual(values=Method_Line_Types)+
scale_shape_manual(values = Method_Shape_Types)+
theme_bw()+guides(colour = guide_legend(nrow = 3))+Theme_special()->p1
ggplot(Final_AMSE_modelMiss |> dplyr::group_by(r2,Method) |>
dplyr::summarise(meanAMSE=mean(AMSE), .groups = 'drop'),
aes(x=factor(r2),y=meanAMSE,color=Method,group=Method,linetype=Method,shape=Method)) +
geom_point()+geom_line()+xlab("Sample size")+ylab("Mean AMSE")+
scale_color_manual(values = Method_Colour)+
scale_linetype_manual(values=Method_Line_Types)+
scale_shape_manual(values = Method_Shape_Types)+
theme_bw()+guides(colour = guide_legend(nrow = 3))+Theme_special()->p2
# ggarrange(p1,p2,nrow = 2,ncol = 1,labels = "auto",
# common.legend = TRUE,legend = "bottom")
p2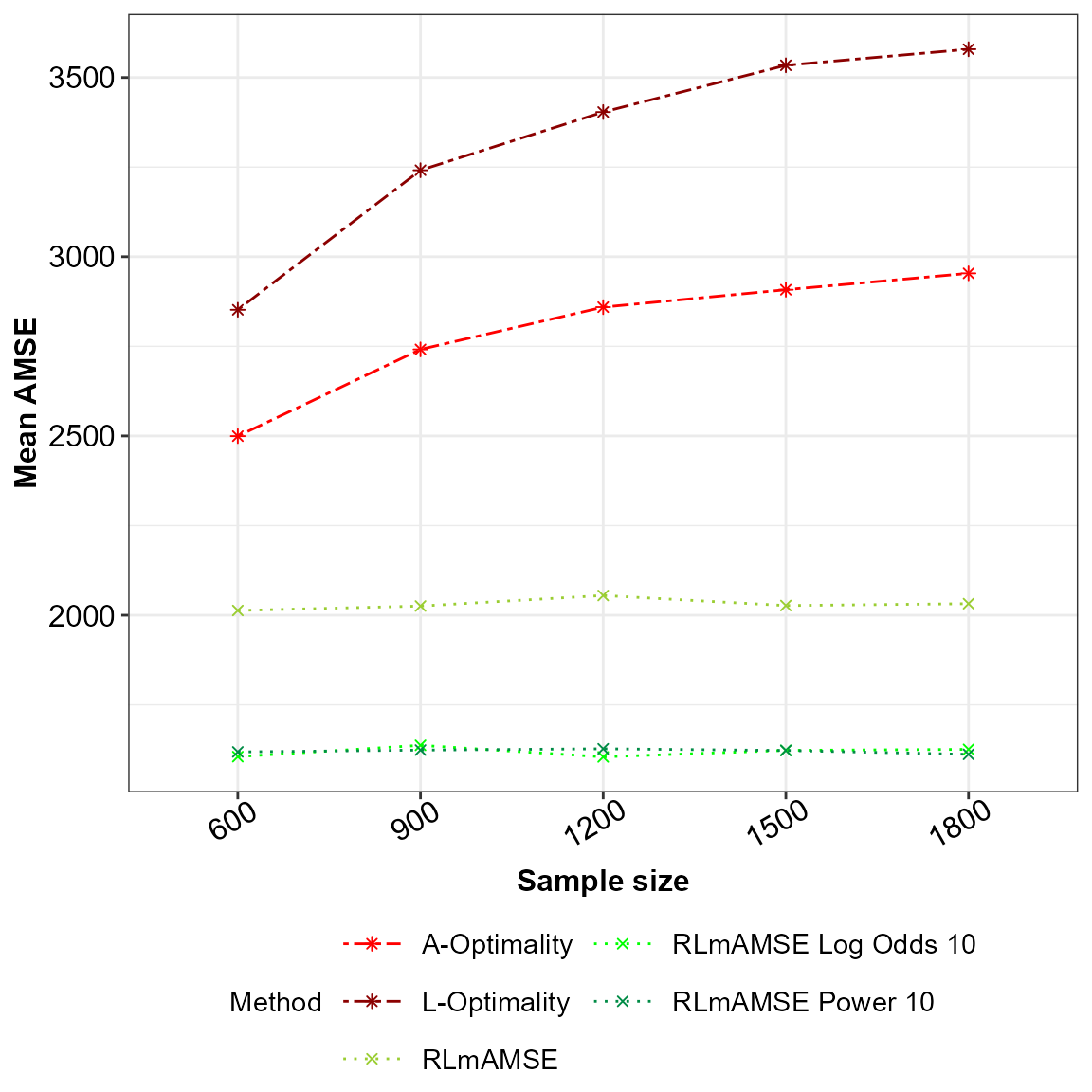
AMSE for the potentially misspecified main effects model across the sampling methods under comparison.