These functions provide the ability for generating probability function values and cumulative probability function values for the COM Poisson Binomial Distribution.
Arguments
- x
vector of binomial random variables.
- n
single value for no of binomial trials.
- p
single value for probability of success.
- v
single value for v.
Value
The output of dCOMPBin gives a list format consisting
pdf probability function values in vector form.
mean mean of COM Poisson Binomial Distribution.
var variance of COM Poisson Binomial Distribution.
Details
The probability function and cumulative function can be constructed and are denoted below
The cumulative probability function is the summation of probability function values.
$$P_{COMPBin}(x) = \frac{{n \choose x}^v p^x (1-p)^{n-x}}{\sum_{j=0}^{n} {n \choose j}^v p^j (1-p)^{(n-j)}}$$ $$x = 0,1,2,3,...n$$ $$n = 1,2,3,...$$ $$0 < p < 1$$ $$-\infty < v < +\infty $$
NOTE : If input parameters are not in given domain conditions necessary error messages will be provided to go further.
References
Borges P, Rodrigues J, Balakrishnan N, Bazan J (2014). “A COM--Poisson type generalization of the binomial distribution and its properties and applications.” Statistics and Probability Letters, 87, 158--166.
Examples
#plotting the random variables and probability values
col <- rainbow(5)
a <- c(0.58,0.59,0.6,0.61,0.62)
b <- c(0.022,0.023,0.024,0.025,0.026)
plot(0,0,main="COM Poisson Binomial probability function graph",xlab="Binomial random variable",
ylab="Probability function values",xlim = c(0,10),ylim = c(0,0.5))
for (i in 1:5)
{
lines(0:10,dCOMPBin(0:10,10,a[i],b[i])$pdf,col = col[i],lwd=2.85)
points(0:10,dCOMPBin(0:10,10,a[i],b[i])$pdf,col = col[i],pch=16)
}
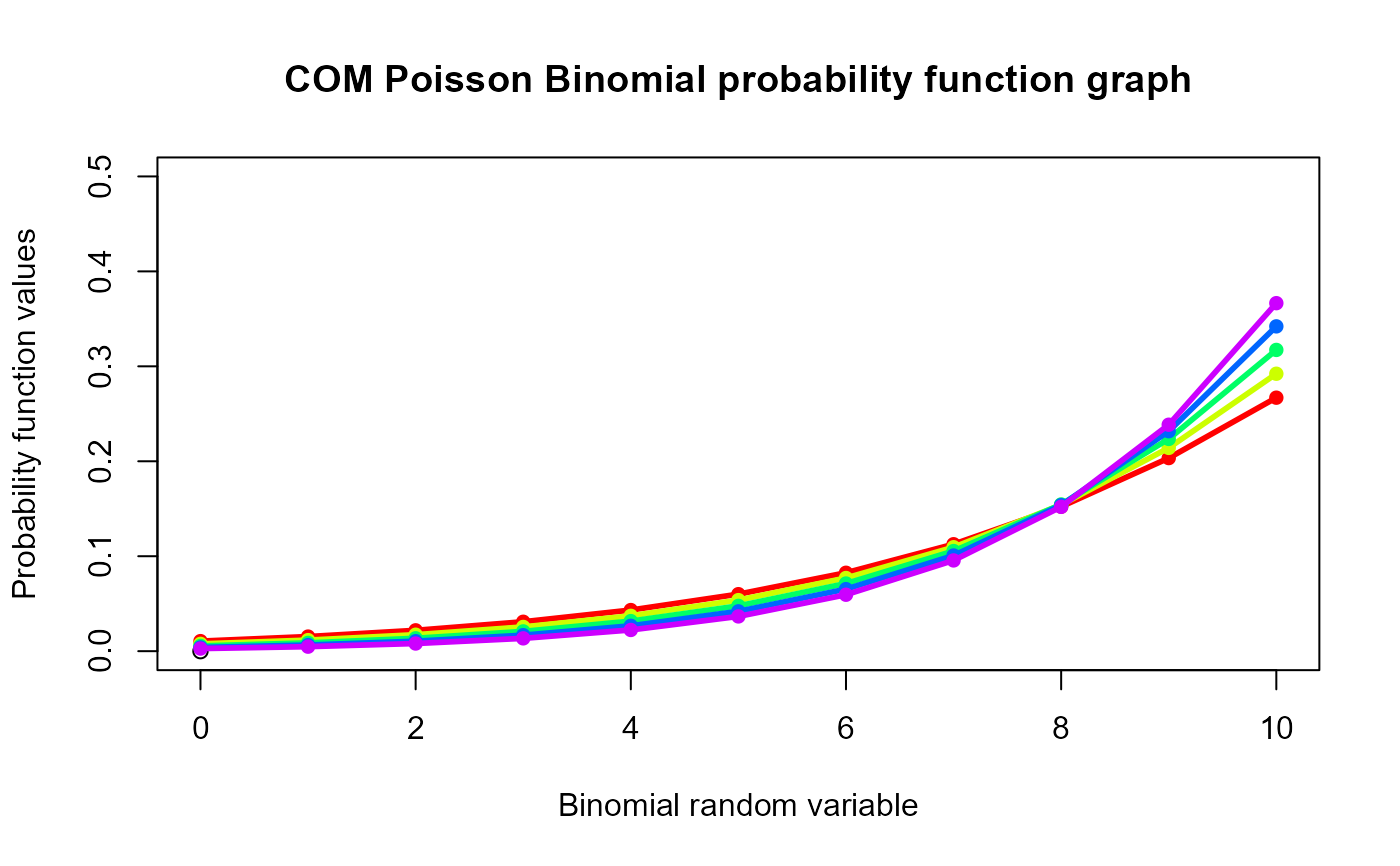dCOMPBin(0:10,10,0.58,0.022)$pdf #extracting the pdf values
#> [1] 0.01058483 0.01537669 0.02194887 0.03097149 0.04329998 0.06003554
#> [7] 0.08257434 0.11263594 0.15222443 0.20337258 0.26697531
dCOMPBin(0:10,10,0.58,0.022)$mean #extracting the mean
#> [1] 7.627366
dCOMPBin(0:10,10,0.58,0.022)$var #extracting the variance
#> [1] 5.803804
#plotting the random variables and cumulative probability values
col <- rainbow(5)
a <- c(0.58,0.59,0.6,0.61,0.62)
b <- c(0.022,0.023,0.024,0.025,0.026)
plot(0,0,main="COM Poisson Binomial probability function graph",xlab="Binomial random variable",
ylab="Probability function values",xlim = c(0,10),ylim = c(0,1))
for (i in 1:5)
{
lines(0:10,pCOMPBin(0:10,10,a[i],b[i]),col = col[i],lwd=2.85)
points(0:10,pCOMPBin(0:10,10,a[i],b[i]),col = col[i],pch=16)
}
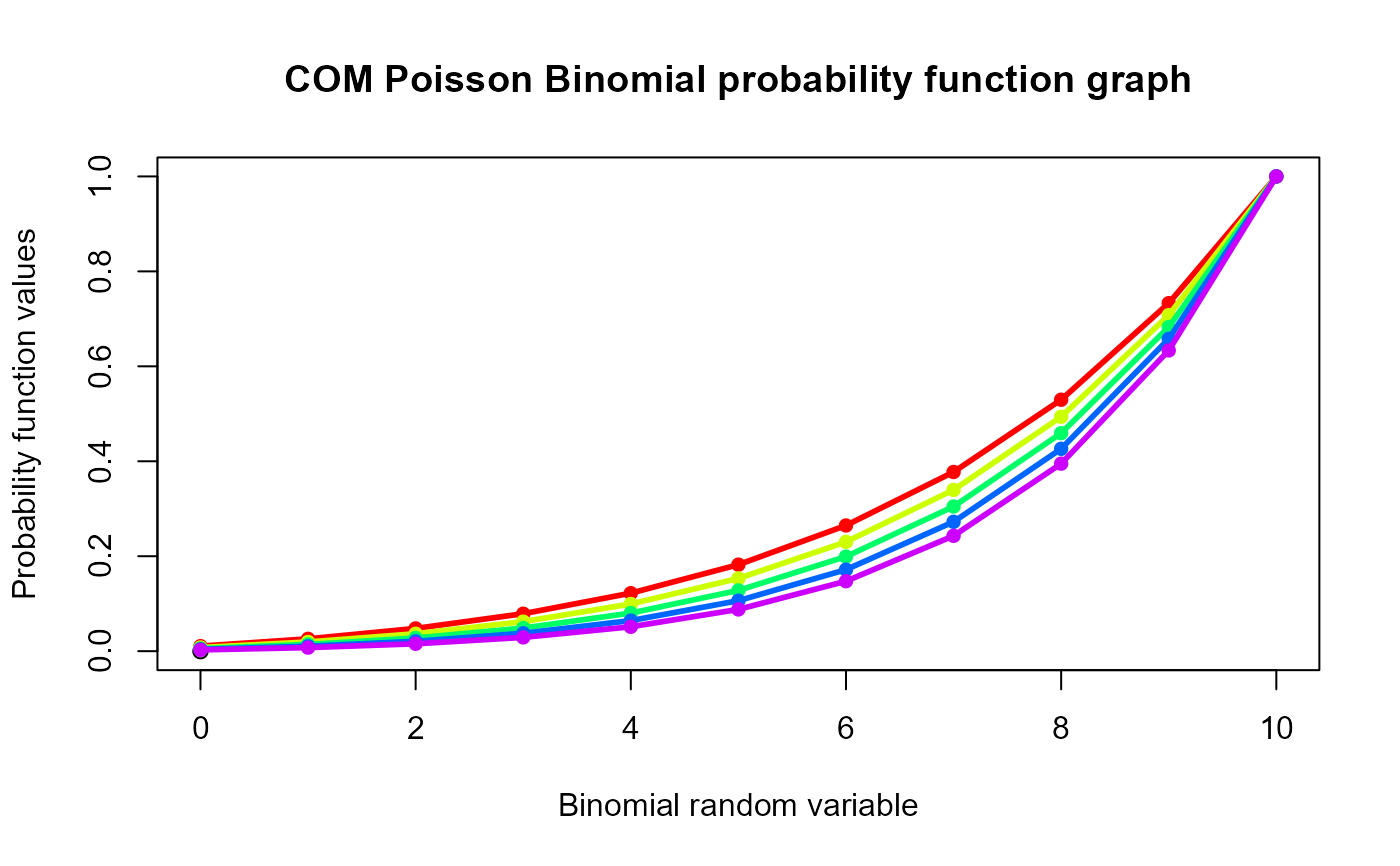pCOMPBin(0:10,10,0.58,0.022) #acquiring the cumulative probability values
#> [1] 0.01058483 0.02596152 0.04791039 0.07888188 0.12218187 0.18221740
#> [7] 0.26479174 0.37742768 0.52965211 0.73302469 1.00000000