These functions provide the ability for generating probability function values and cumulative probability function values for the Beta-Correlated Binomial Distribution.
Arguments
- x
vector of binomial random variables.
- n
single value for no of binomial trials.
- cov
single value for covariance.
- a
single value for alpha parameter
- b
single value for beta parameter.
Details
The probability function and cumulative function can be constructed and are denoted below
The cumulative probability function is the summation of probability function values.
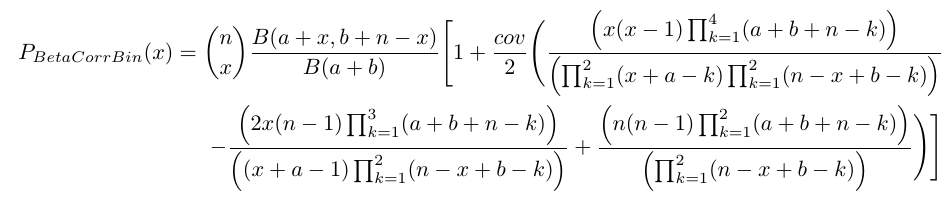
$$x = 0,1,2,3,...n$$ $$n = 1,2,3,...$$ $$-\infty < cov < +\infty $$ $$0< a,b$$ $$0 < p < 1$$
$$p=\frac{a}{a+b}$$ $$\Theta=\frac{1}{a+b}$$
The Correlation is in between $$\frac{-2}{n(n-1)} min(\frac{p}{1-p},\frac{1-p}{p}) \le correlation \le \frac{2p(1-p)}{(n-1)p(1-p)+0.25-fo} $$ where \(fo=min (x-(n-1)p-0.5)^2 \)
The mean and the variance are denoted as $$E_{BetaCorrBin}[x]= np$$ $$Var_{BetaCorrBin}[x]= np(1-p)(n\Theta+1)(1+\Theta)^{-1}+n(n-1)cov$$ $$Corr_{BetaCorrBin}[x]=\frac{cov}{p(1-p)}$$
NOTE : If input parameters are not in given domain conditions necessary error messages will be provided to go further.
References
Paul SR (1985). “A three-parameter generalization of the binomial distribution.” History and Philosophy of Logic, 14(6), 1497--1506.
Examples
#plotting the random variables and probability values
col <- rainbow(5)
a <- c(9.0,10,11,12,13)
b <- c(8.0,8.1,8.2,8.3,8.4)
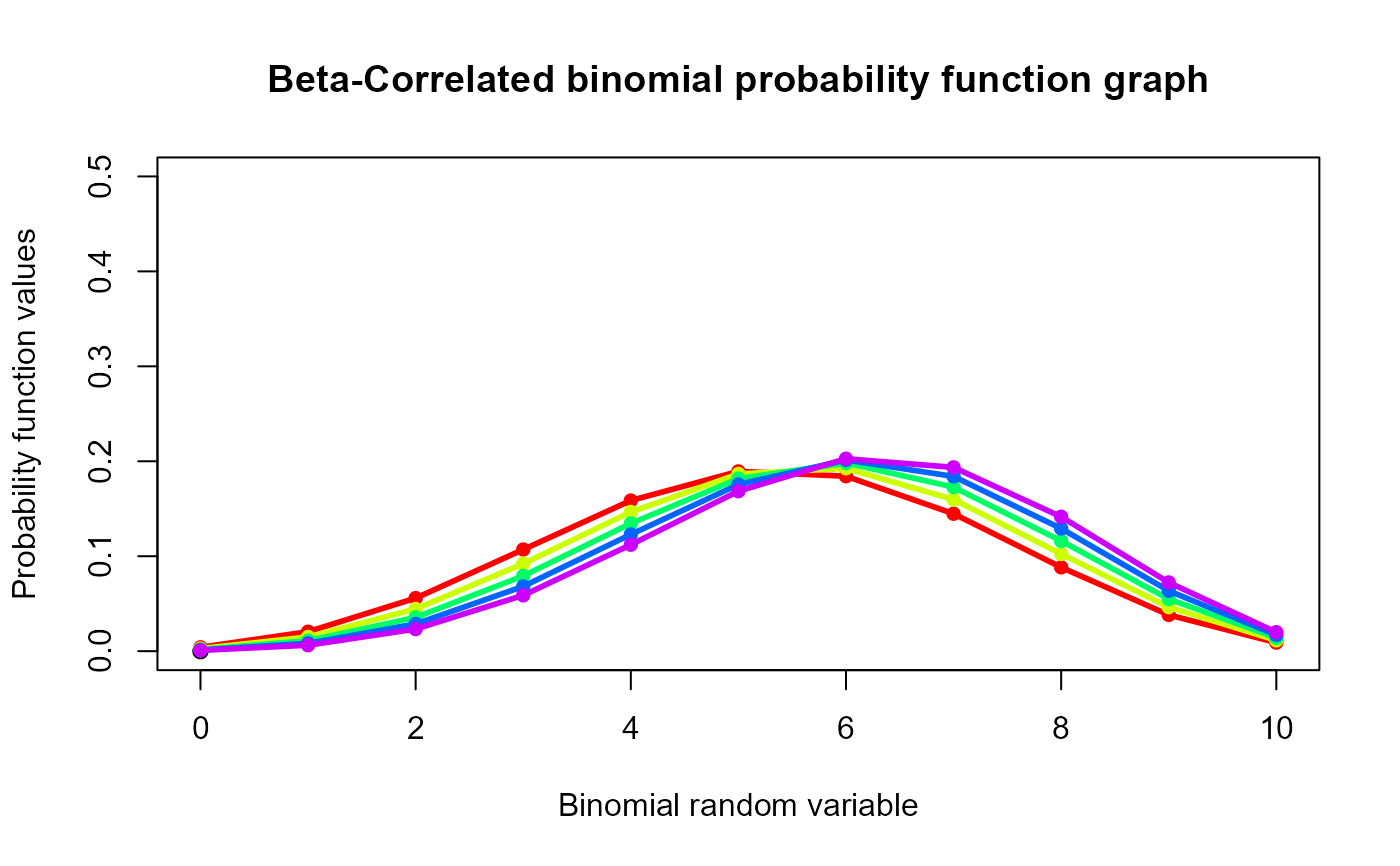
plot(0,0,main="Beta-Correlated binomial probability function graph",xlab="Binomial random variable",
ylab="Probability function values",xlim = c(0,10),ylim = c(0,0.5))
for (i in 1:5)
{
lines(0:10,dBetaCorrBin(0:10,10,0.001,a[i],b[i])$pdf,col = col[i],lwd=2.85)
points(0:10,dBetaCorrBin(0:10,10,0.001,a[i],b[i])$pdf,col = col[i],pch=16)
}
dBetaCorrBin(0:10,10,0.001,10,13)$pdf #extracting the pdf values
#> [1] 0.010992133 0.047498928 0.108466364 0.170474118 0.202669472 0.189491674
#> [7] 0.140699312 0.081828892 0.035693121 0.010567136 0.001618852
dBetaCorrBin(0:10,10,0.001,10,13)$mean #extracting the mean
#> [1] 4.347826
dBetaCorrBin(0:10,10,0.001,10,13)$var #extracting the variance
#> [1] 3.469017
dBetaCorrBin(0:10,10,0.001,10,13)$corr #extracting the correlation
#> [1] 0.004069231
dBetaCorrBin(0:10,10,0.001,10,13)$mincorr #extracting the minimum correlation value
#> [1] -0.01709402
dBetaCorrBin(0:10,10,0.001,10,13)$maxcorr #extracting the maximum correlation value
#> [1] 0.2145215
#plotting the random variables and cumulative probability values
col <- rainbow(5)
a <- c(9.0,10,11,12,13)
b <- c(8.0,8.1,8.2,8.3,8.4)
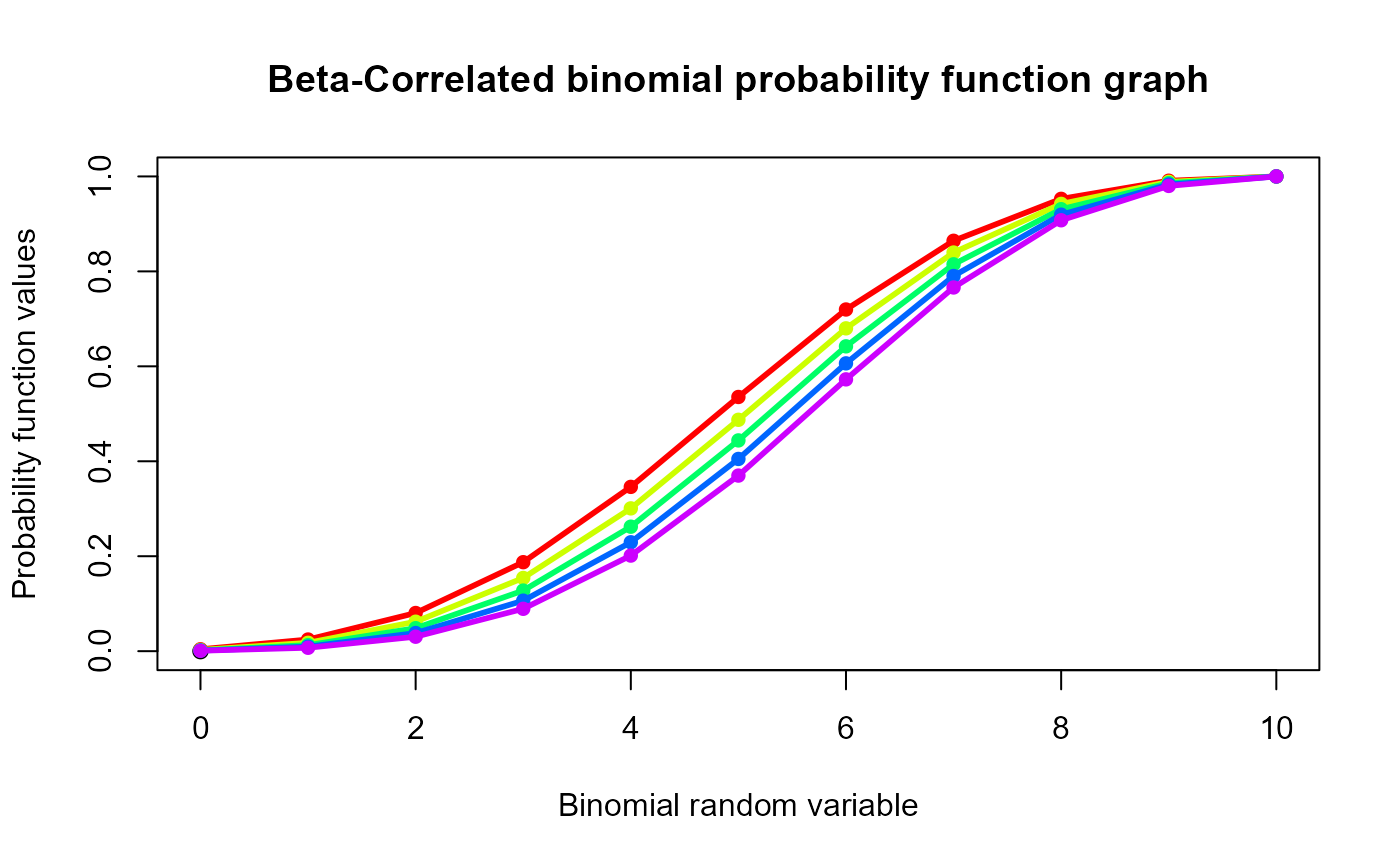
plot(0,0,main="Beta-Correlated binomial probability function graph",xlab="Binomial random variable",
ylab="Probability function values",xlim = c(0,10),ylim = c(0,1))
for (i in 1:5)
{
lines(0:10,pBetaCorrBin(0:10,10,0.001,a[i],b[i]),col = col[i],lwd=2.85)
points(0:10,pBetaCorrBin(0:10,10,0.001,a[i],b[i]),col = col[i],pch=16)
}
pBetaCorrBin(0:10,10,0.001,10,13) #acquiring the cumulative probability values
#> [1] 0.01099213 0.05849106 0.16695742 0.33743154 0.54010101 0.72959269
#> [7] 0.87029200 0.95212089 0.98781401 0.99838115 1.00000000