These functions provide the ability for generating probability density values, cumulative probability density values and moments about zero values for the Triangular Distribution bounded between [0,1].
Details
Setting \(min=0\) and \(max=1\) \(mode=c\) in the Triangular distribution a unit bounded Triangular distribution can be obtained. The probability density function and cumulative density function of a unit bounded Triangular distribution with random variable P are given by
$$g_{P}(p)= \frac{2p}{c} $$ ; \(0 \le p < c\) $$g_{P}(p)= \frac{2(1-p)}{(1-c)} $$ ; \(c \le p \le 1\) $$G_{P}(p)= \frac{p^2}{c} $$ ; \(0 \le p < c\) $$G_{P}(p)= 1-\frac{(1-p)^2}{(1-c)} $$ ; \(c \le p \le 1\) $$0 \le mode=c \le 1$$
The mean and the variance are denoted by $$E[P]= \frac{(a+b+c)}{3}= \frac{(1+c)}{3} $$ $$var[P]= \frac{a^2+b^2+c^2-ab-ac-bc}{18}= \frac{(1+c^2-c)}{18} $$
Moments about zero is denoted as $$E[P^r]= \frac{2c^{r+2}}{c(r+2)}+\frac{2(1-c^{r+1})}{(1-c)(r+1)}+\frac{2(c^{r+2}-1)}{(1-c)(r+2)} $$ \(r = 1,2,3,...\)
NOTE : If input parameters are not in given domain conditions necessary error messages will be provided to go further.
References
Horsnell G (1957). “Economical acceptance sampling schemes.” Journal of the Royal Statistical Society. Series A (General), 120(2), 148--201. Johnson NL, Kotz S, Balakrishnan N (1995). Continuous univariate distributions, volume 2, volume 289. John wiley and sons. Karlis D, Xekalaki E (2008). The polygonal distribution. Springer. Okagbue HI, Edeki SO, Opanuga AA, Oguntunde PE, Adeosun ME (2014). “Using the Average of the Extreme Values of a Triangular Distribution for a Transformation, and Its Approximant via the Continuous Uniform Distribution.” British Journal of Mathematics and Computer Science, 4(24), 3497.
Examples
#plotting the random variables and probability values
col <- rainbow(4)
x <- seq(0.2,0.8,by=0.2)
plot(0,0,main="Probability density graph",xlab="Random variable",
ylab="Probability density values",xlim = c(0,1),ylim = c(0,3))
for (i in 1:4)
{
lines(seq(0,1,by=0.01),dTRI(seq(0,1,by=0.01),x[i])$pdf,col = col[i])
}
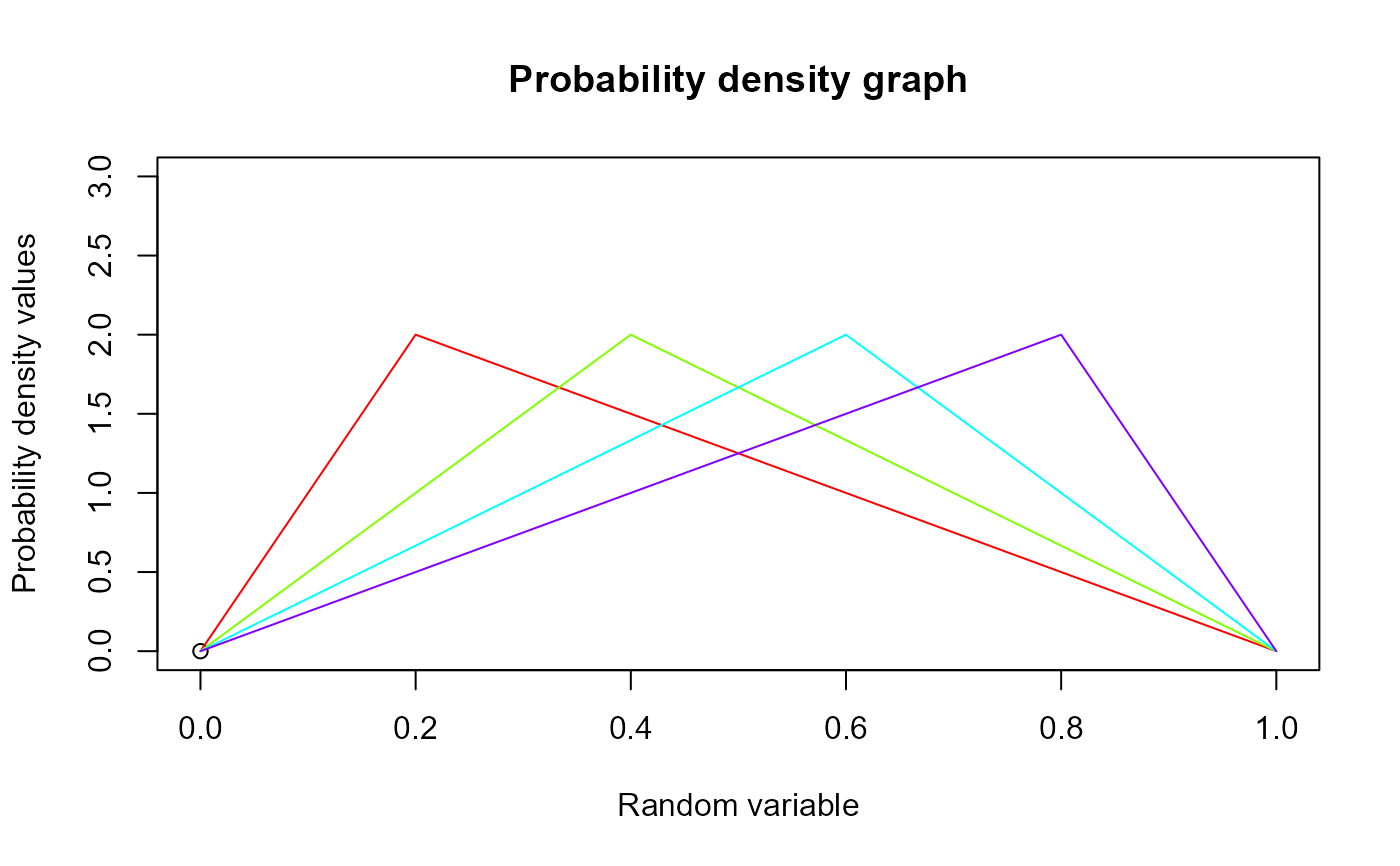dTRI(seq(0,1,by=0.05),0.3)$pdf #extracting the pdf values
#> [1] 0.0000000 0.3333333 0.6666667 1.0000000 1.3333333 1.6666667 2.0000000
#> [8] 1.8571429 1.7142857 1.5714286 1.4285714 1.2857143 1.1428571 1.0000000
#> [15] 0.8571429 0.7142857 0.5714286 0.4285714 0.2857143 0.1428571 0.0000000
dTRI(seq(0,1,by=0.01),0.3)$mean #extracting the mean
#> [1] 0.4333333
dTRI(seq(0,1,by=0.01),0.3)$var #extracting the variance
#> [1] 0.04388889
#plotting the random variables and cumulative probability values
col <- rainbow(4)
x <- seq(0.2,0.8,by=0.2)
plot(0,0,main="Cumulative density graph",xlab="Random variable",
ylab="Cumulative density values",xlim = c(0,1),ylim = c(0,1))
for (i in 1:4)
{
lines(seq(0,1,by=0.01),pTRI(seq(0,1,by=0.01),x[i]),col = col[i])
}
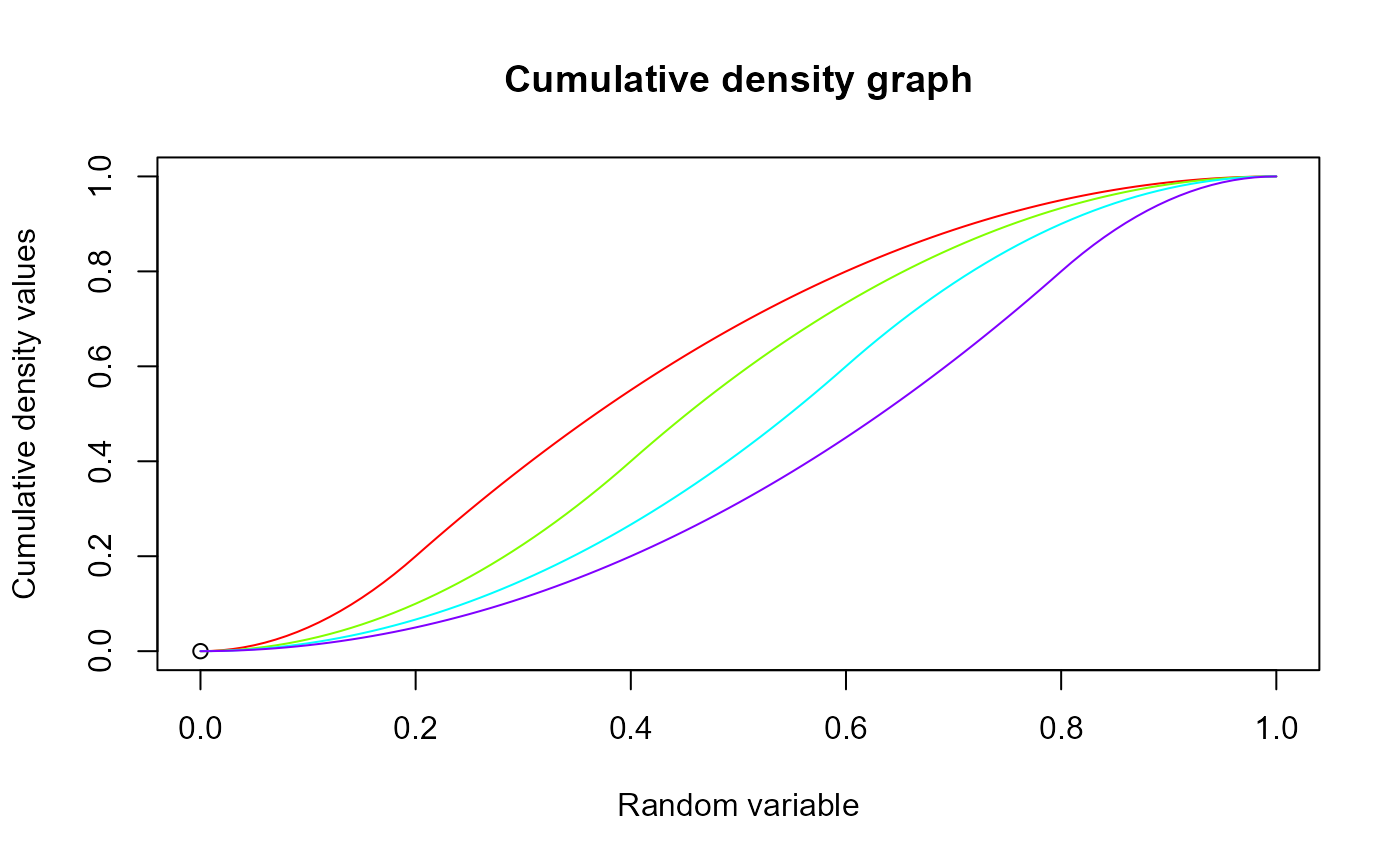pTRI(seq(0,1,by=0.05),0.3) #acquiring the cumulative probability values
#> [1] 0.000000000 0.008333333 0.033333333 0.075000000 0.133333333 0.208333333
#> [7] 0.300000000 0.396428571 0.485714286 0.567857143 0.642857143 0.710714286
#> [13] 0.771428571 0.825000000 0.871428571 0.910714286 0.942857143 0.967857143
#> [19] 0.985714286 0.996428571 1.000000000
mazTRI(1.4,.3) #acquiring the moment about zero values
#> [1] 0.4333333
mazTRI(2,.3)-mazTRI(1,.3)^2 #variance for when is mode 0.3
#> [1] 0.04388889
#only the integer value of moments is taken here because moments cannot be decimal
mazTRI(1.9,0.5)
#> [1] 0.5