Beta-Binomial Distribution

Source: R/Beta.R

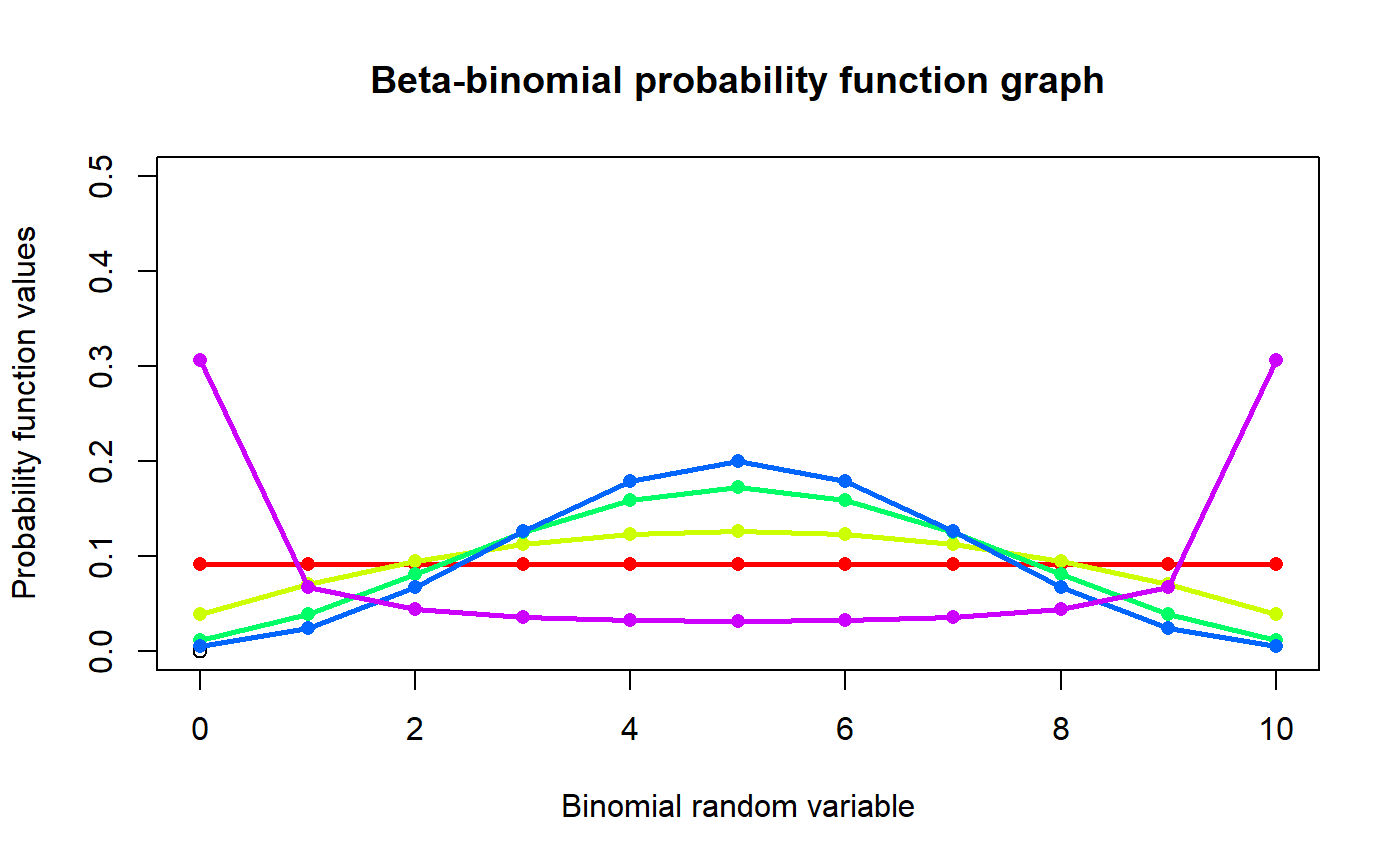
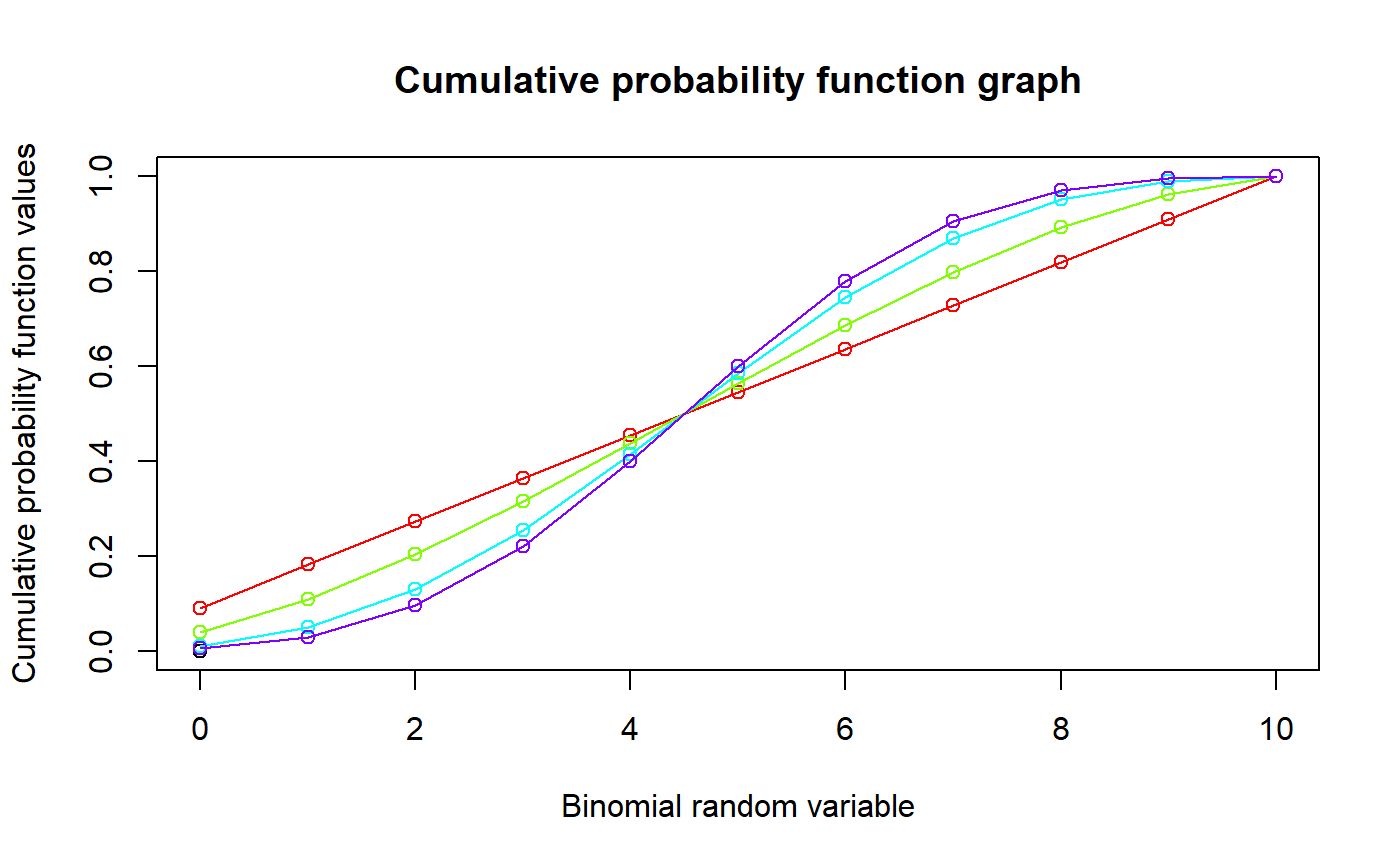
These functions provide the ability for generating probability function values and cumulative probability function values for the Beta-Binomial Distribution.

pBetaBin(x,n,a,b)

Arguments

x

vector of binomial random variables.
n

single value for no of binomial trials.
a

single value for shape parameter alpha representing as a.
b

single value for shape parameter beta representing as b.

Value

The output of pBetaBin gives cumulative probability values in vector form.

Details

Mixing Beta distribution with Binomial distribution will create the Beta-Binomial distribution. The probability function and cumulative probability function can be constructed and are denoted below.

The cumulative probability function is the summation of probability function values.

$$P_{BetaBin}(x)= {n \choose x} \frac{B(a+x,n+b-x)}{B(a,b)} $$ $$a,b > 0$$ $$x = 0,1,2,3,...n$$ $$n = 1,2,3,...$$

The mean, variance and over dispersion are denoted as $$E_{BetaBin}[x]= \frac{na}{a+b} $$ $$Var_{BetaBin}[x]= \frac{(nab)}{(a+b)^2} \frac{(a+b+n)}{(a+b+1)} $$ $$over dispersion= \frac{1}{a+b+1} $$

Defined as B(a,b) is the beta function.

References

Young-Xu, Y. & Chan, K.A., 2008. Pooling overdispersed binomial data to estimate event rate. BMC medical research methodology, 8(1), p.58.

Available at: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2538541&tool=pmcentrez&rendertype=abstract.

Trenkler, G., 1996. Continuous univariate distributions. Computational Statistics & Data Analysis, 21(1), p.119.

Available at: http://linkinghub.elsevier.com/retrieve/pii/0167947396900158.

Hughes, G., 1993. Using the Beta-Binomial Distribution to Describe Aggregated Patterns of Disease Incidence. Phytopathology, 83(9), p.759.

Available at: http://www.apsnet.org/publications/phytopathology/backissues/Documents/1993Abstracts/Phyto_83_759.htm

Examples

#plotting the random variables and probability values
col <- rainbow(5)
a <- c(1,2,5,10,0.2)
plot(0,0,main="Beta-binomial probability function graph",xlab="Binomial random variable",
ylab="Probability function values",xlim = c(0,10),ylim = c(0,0.5))
for (i in 1:5)
{
lines(0:10,dBetaBin(0:10,10,a[i],a[i])$pdf,col = col[i],lwd=2.85)
points(0:10,dBetaBin(0:10,10,a[i],a[i])$pdf,col = col[i],pch=16)
}

dBetaBin(0:10,10,4,.2)$pdf    #extracting the pdf values
#>  [1] 9.184001e-05 3.993044e-04 1.095652e-03 2.434783e-03 4.810660e-03
#>  [6] 8.881218e-03 1.585932e-02 2.832021e-02 5.310040e-02 1.180009e-01
#> [11] 7.670057e-01
dBetaBin(0:10,10,4,.2)$mean   #extracting the mean
#> [1] 9.52381
dBetaBin(0:10,10,4,.2)$var    #extracting the variance
#> [1] 1.238444
dBetaBin(0:10,10,4,.2)$over.dis.para  #extracting the over dispersion value
#> [1] 0.1923077

#plotting the random variables and cumulative probability values
col <- rainbow(4)
a <- c(1,2,5,10)
plot(0,0,main="Cumulative probability function graph",xlab="Binomial random variable",
ylab="Cumulative probability function values",xlim = c(0,10),ylim = c(0,1))
for (i in 1:4)
{
lines(0:10,pBetaBin(0:10,10,a[i],a[i]),col = col[i])
points(0:10,pBetaBin(0:10,10,a[i],a[i]),col = col[i])
}

pBetaBin(0:10,10,4,.2)   #acquiring the cumulative probability values
#>  [1] 9.184001e-05 4.911444e-04 1.586797e-03 4.021580e-03 8.832240e-03
#>  [6] 1.771346e-02 3.357278e-02 6.189299e-02 1.149934e-01 2.329943e-01
#> [11] 1.000000e+00