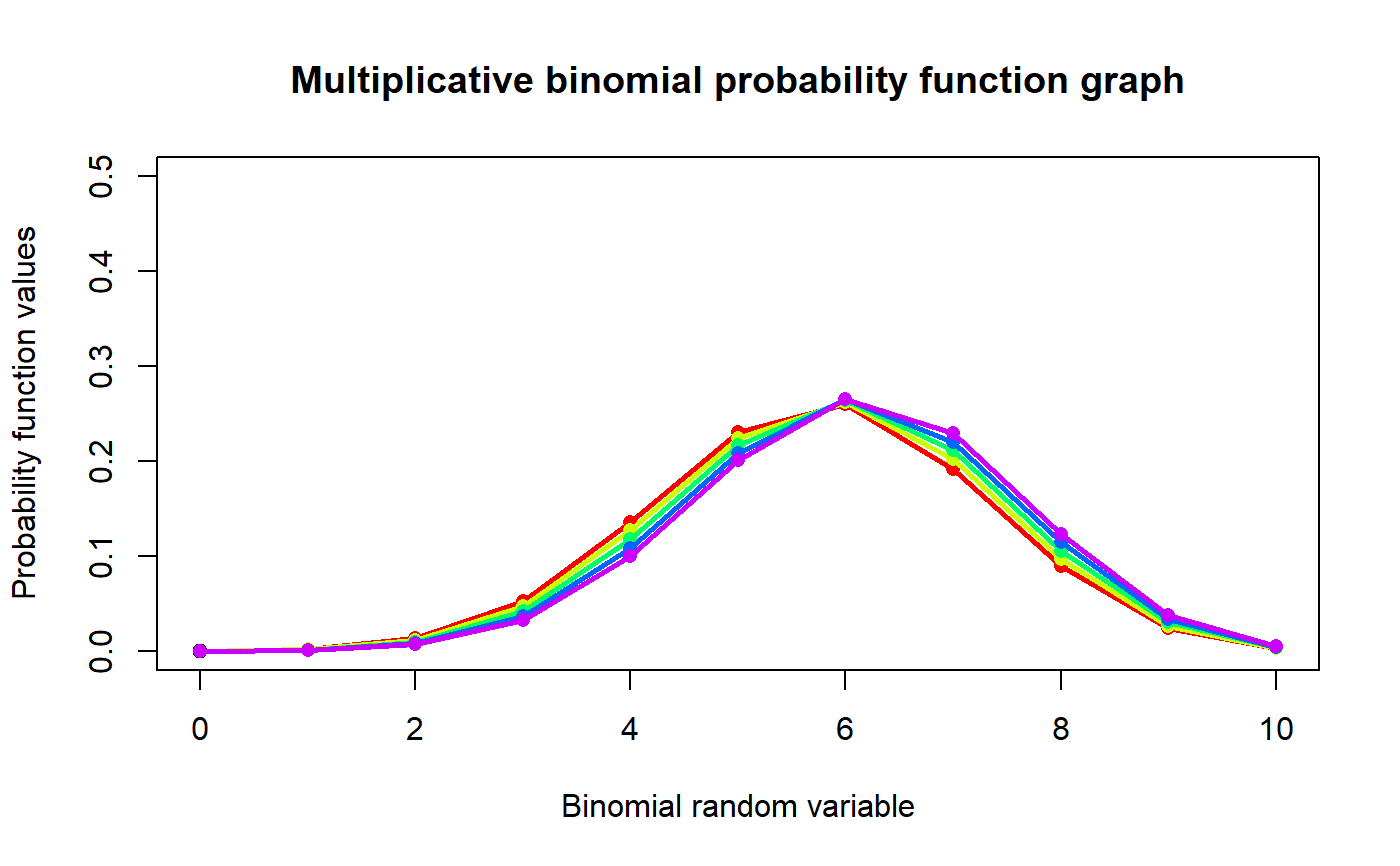
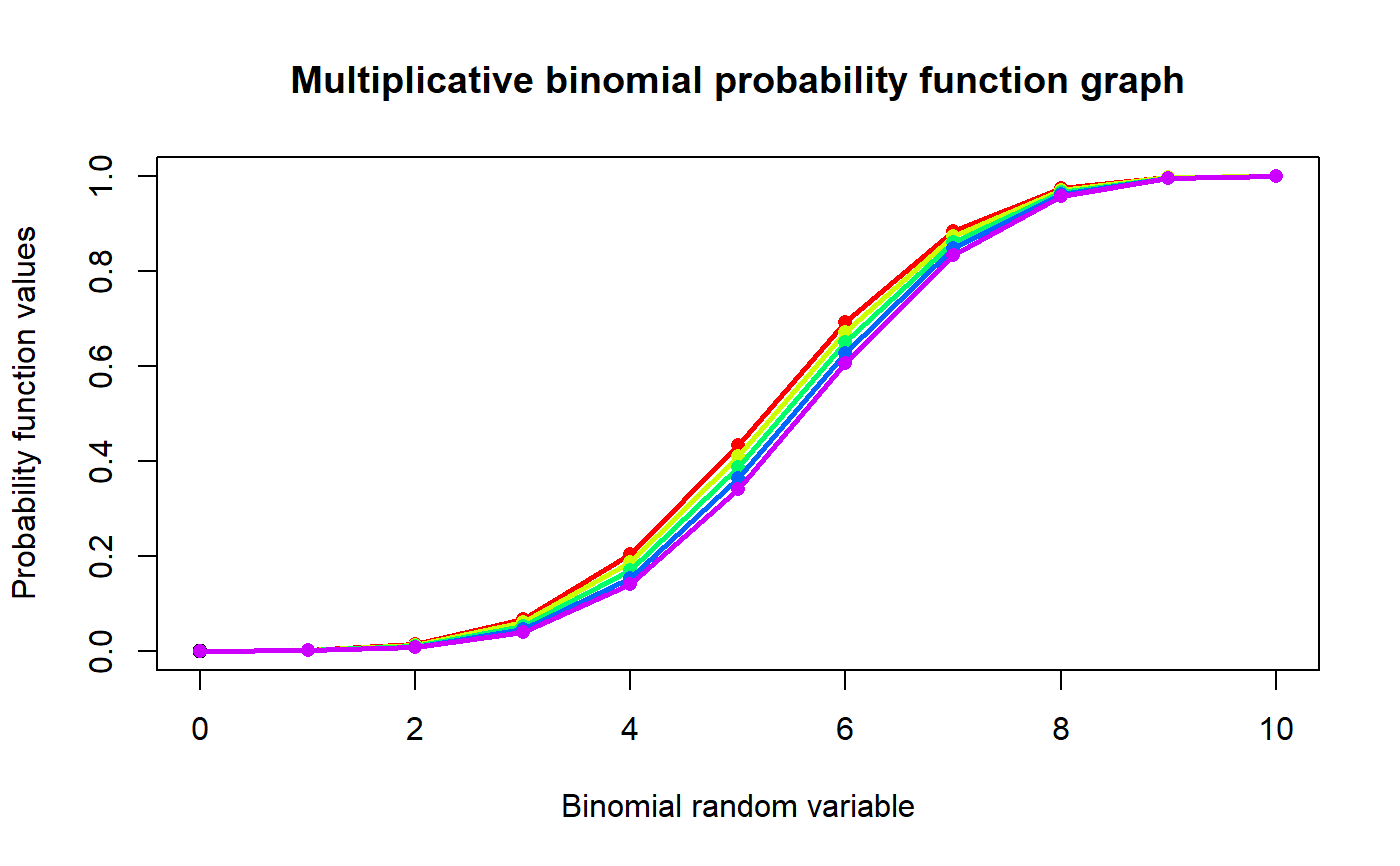
Multiplicative Binomial Distribution

Source: R/MultiBin.R

These functions provide the ability for generating probability function values and cumulative probability function values for the Multiplicative Binomial Distribution.

dMultiBin(x,n,p,theta)

Arguments

x

vector of binomial random variables.
n

single value for no of binomial trials.
p

single value for probability of success.
theta

single value for theta.

Value

The output of dMultiBin gives a list format consisting

pdf probability function values in vector form.

mean mean of Multiplicative Binomial Distribution.

var variance of Multiplicative Binomial Distribution.

Details

The probability function and cumulative function can be constructed and are denoted below

The cumulative probability function is the summation of probability function values.

$$P_{MultiBin}(x)= {n \choose x} p^x (1-p)^{n-x} \frac{(theta^{x(n-x)}}{f(p,theta,n)} $$

here \(f(p,theta,n)\) is $$f(p,theta,n)= \sum_{k=0}^{n} {n \choose k} p^k (1-p)^{n-k} (theta^{k(n-k)} )$$

$$x = 0,1,2,3,...n$$ $$n = 1,2,3,...$$ $$k = 0,1,2,...,n$$ $$0 < p < 1$$ $$0 < theta $$

NOTE : If input parameters are not in given domain conditions necessary error messages will be provided to go further.

References

Johnson, N. L., Kemp, A. W., & Kotz, S. (2005). Univariate discrete distributions (Vol. 444). Hoboken, NJ: Wiley-Interscience.

L. L. Kupper, J.K.H., 1978. The Use of a Correlated Binomial Model for the Analysis of Certain Toxicological Experiments. Biometrics, 34(1), pp.69-76.

Paul, S.R., 1985. A three-parameter generalization of the binomial distribution. Communications in Statistics - Theory and Methods, 14(6), pp.1497-1506.

Available at: http://www.tandfonline.com/doi/abs/10.1080/03610928508828990.

Examples

#plotting the random variables and probability values
col <- rainbow(5)
a <- c(0.58,0.59,0.6,0.61,0.62)
b <- c(0.022,0.023,0.024,0.025,0.026)
plot(0,0,main="Multiplicative binomial probability function graph",xlab="Binomial random variable",
ylab="Probability function values",xlim = c(0,10),ylim = c(0,0.5))
for (i in 1:5)
{
lines(0:10,dMultiBin(0:10,10,a[i],1+b[i])$pdf,col = col[i],lwd=2.85)
points(0:10,dMultiBin(0:10,10,a[i],1+b[i])$pdf,col = col[i],pch=16)
}

dMultiBin(0:10,10,.58,10.022)$pdf   #extracting the pdf values
#>  [1] 6.364309e-29 8.964365e-19 5.657070e-11 2.106255e-05 5.123785e-02
#>  [6] 8.509524e-01 9.771209e-02 7.659947e-05 3.923411e-10 1.185630e-17
#> [11] 1.605234e-27
dMultiBin(0:10,10,.58,10.022)$mean   #extracting the mean
#> [1] 5.046585
dMultiBin(0:10,10,.58,10.022)$var   #extracting the variance
#> [1] 0.1471704


#plotting random variables and cumulative probability values
col <- rainbow(5)
a <- c(0.58,0.59,0.6,0.61,0.62)
b <- c(0.022,0.023,0.024,0.025,0.026)
plot(0,0,main="Multiplicative binomial probability function graph",xlab="Binomial random variable",
ylab="Probability function values",xlim = c(0,10),ylim = c(0,1))
for (i in 1:5)
{
lines(0:10,pMultiBin(0:10,10,a[i],1+b[i]),col = col[i],lwd=2.85)
points(0:10,pMultiBin(0:10,10,a[i],1+b[i]),col = col[i],pch=16)
}

pMultiBin(0:10,10,.58,10.022)     #acquiring the cumulative probability values
#>  [1] 6.364309e-29 8.964365e-19 5.657070e-11 2.106261e-05 5.125891e-02
#>  [6] 9.022113e-01 9.999234e-01 1.000000e+00 1.000000e+00 1.000000e+00
#> [11] 1.000000e+00