Beta Distribution

Source: R/Beta.R

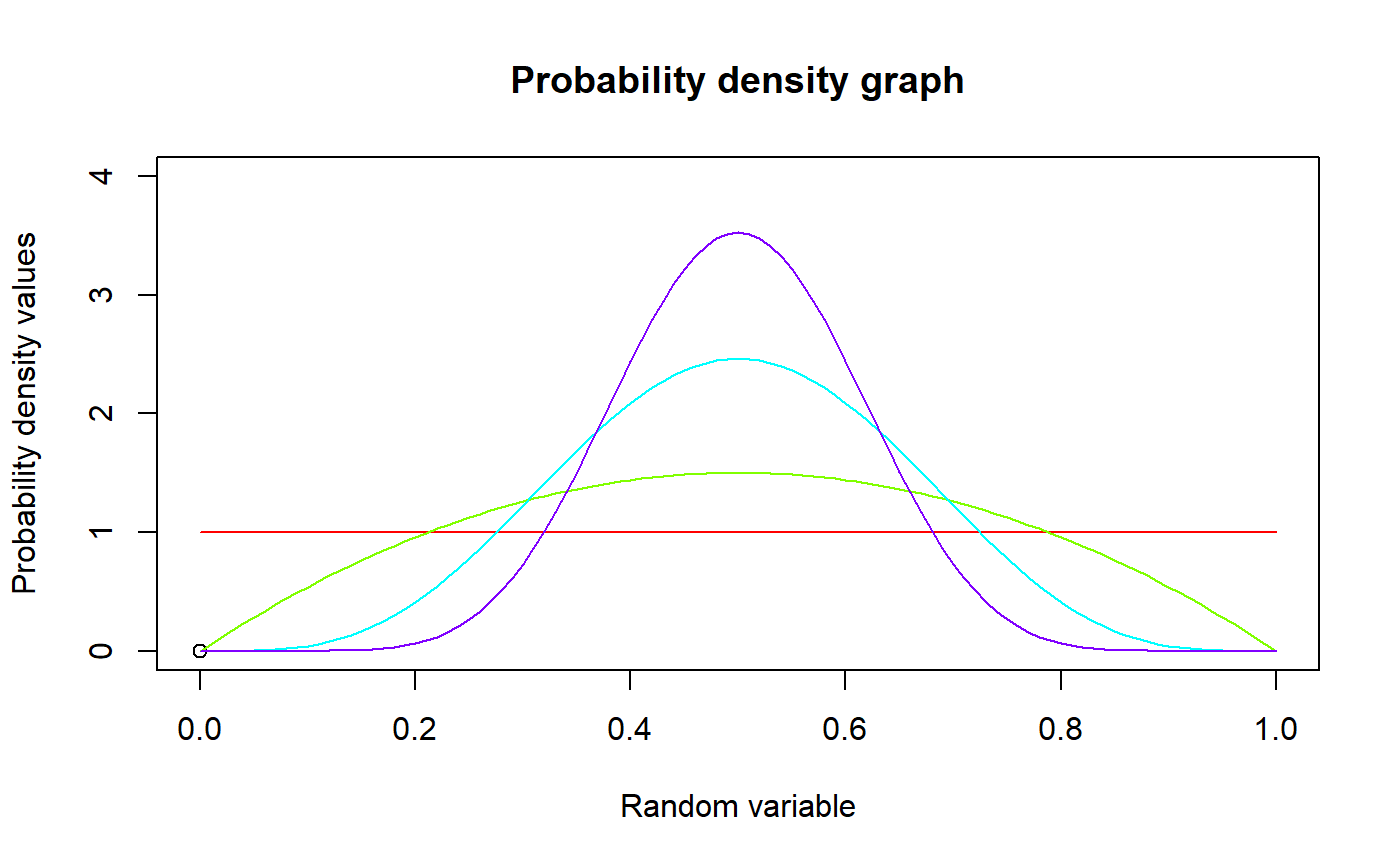
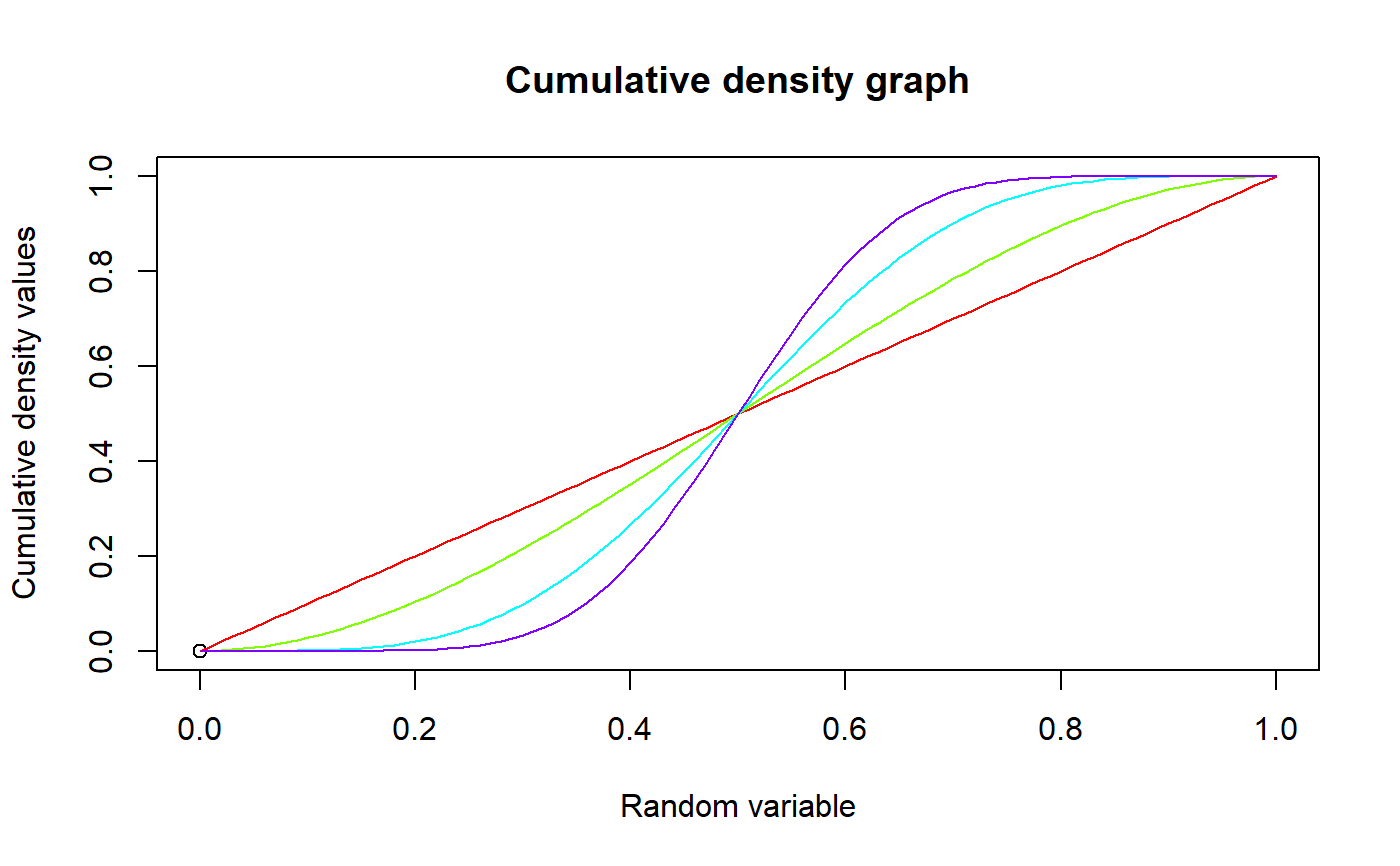
These functions provide the ability for generating probability density values, cumulative probability density values and moment about zero values for the Beta Distribution bounded between [0,1]

dBETA(p,a,b)

Arguments

p

vector of probabilities.
a

single value for shape parameter alpha representing as a.
b

single value for shape parameter beta representing as b.

Value

The output of dBETA gives a list format consisting

pdf probability density values in vector form.

mean mean of the Beta distribution.

var variance of the Beta distribution.

Details

The probability density function and cumulative density function of a unit bounded Beta distribution with random variable P are given by

$$g_{P}(p)= \frac{p^{a-1}(1-p)^{b-1}}{B(a,b)} $$ ; \(0 \le p \le 1\) $$G_{P}(p)= \frac{B_p(a,b)}{B(a,b)} $$ ; \(0 \le p \le 1\) $$a,b > 0$$

The mean and the variance are denoted by $$E[P]= \frac{a}{a+b} $$ $$var[P]= \frac{ab}{(a+b)^2(a+b+1)} $$

The moments about zero is denoted as $$E[P^r]= \prod_{i=0}^{r-1} (\frac{a+i}{a+b+i}) $$ \(r = 1,2,3,...\)

Defined as \(B_p(a,b)=\int^p_0 t^{a-1} (1-t)^{b-1}\,dt\) is incomplete beta integrals and \(B(a,b)\) is the beta function.

NOTE : If input parameters are not in given domain conditions necessary error messages will be provided to go further.

References

Johnson, N. L., Kotz, S. and Balakrishnan, N. (1994) Continuous Univariate Distributions, Vol. 2, Wiley Series in Probability and Mathematical Statistics, Wiley.

Trenkler, G., 1996. Continuous univariate distributions. Computational Statistics & Data Analysis, 21(1), p.119.

Available at: http://linkinghub.elsevier.com/retrieve/pii/0167947396900158.

See also

Beta

or

https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Beta.html

Examples

#plotting the random variables and probability values
col <- rainbow(4)
a <- c(1,2,5,10)
plot(0,0,main="Probability density graph",xlab="Random variable",ylab="Probability density values",
xlim = c(0,1),ylim = c(0,4))
for (i in 1:4)
{
lines(seq(0,1,by=0.01),dBETA(seq(0,1,by=0.01),a[i],a[i])$pdf,col = col[i])
}

dBETA(seq(0,1,by=0.01),2,3)$pdf   #extracting the pdf values
#>   [1] 0.000000 0.117612 0.230496 0.338724 0.442368 0.541500 0.636192 0.726516
#>   [9] 0.812544 0.894348 0.972000 1.045572 1.115136 1.180764 1.242528 1.300500
#>  [17] 1.354752 1.405356 1.452384 1.495908 1.536000 1.572732 1.606176 1.636404
#>  [25] 1.663488 1.687500 1.708512 1.726596 1.741824 1.754268 1.764000 1.771092
#>  [33] 1.775616 1.777644 1.777248 1.774500 1.769472 1.762236 1.752864 1.741428
#>  [41] 1.728000 1.712652 1.695456 1.676484 1.655808 1.633500 1.609632 1.584276
#>  [49] 1.557504 1.529388 1.500000 1.469412 1.437696 1.404924 1.371168 1.336500
#>  [57] 1.300992 1.264716 1.227744 1.190148 1.152000 1.113372 1.074336 1.034964
#>  [65] 0.995328 0.955500 0.915552 0.875556 0.835584 0.795708 0.756000 0.716532
#>  [73] 0.677376 0.638604 0.600288 0.562500 0.525312 0.488796 0.453024 0.418068
#>  [81] 0.384000 0.350892 0.318816 0.287844 0.258048 0.229500 0.202272 0.176436
#>  [89] 0.152064 0.129228 0.108000 0.088452 0.070656 0.054684 0.040608 0.028500
#>  [97] 0.018432 0.010476 0.004704 0.001188 0.000000
dBETA(seq(0,1,by=0.01),2,3)$mean  #extracting the mean
#> [1] 0.4
dBETA(seq(0,1,by=0.01),2,3)$var   #extracting the variance
#> [1] 0.04

#plotting the random variables and cumulative probability values
col <- rainbow(4)
a <- c(1,2,5,10)
plot(0,0,main="Cumulative density graph",xlab="Random variable",ylab="Cumulative density values",
xlim = c(0,1),ylim = c(0,1))
for (i in 1:4)
{
lines(seq(0,1,by=0.01),pBETA(seq(0,1,by=0.01),a[i],a[i]),col = col[i])
}

pBETA(seq(0,1,by=0.01),2,3)   #acquiring the cumulative probability values
#>   [1] 0.00000000 0.00059203 0.00233648 0.00518643 0.00909568 0.01401875
#>   [7] 0.01991088 0.02672803 0.03442688 0.04296483 0.05230000 0.06239123
#>  [13] 0.07319808 0.08468083 0.09680048 0.10951875 0.12279808 0.13660163
#>  [19] 0.15089328 0.16563763 0.18080000 0.19634643 0.21224368 0.22845923
#>  [25] 0.24496128 0.26171875 0.27870128 0.29587923 0.31322368 0.33070643
#>  [31] 0.34830000 0.36597763 0.38371328 0.40148163 0.41925808 0.43701875
#>  [37] 0.45474048 0.47240083 0.48997808 0.50745123 0.52480000 0.54200483
#>  [43] 0.55904688 0.57590803 0.59257088 0.60901875 0.62523568 0.64120643
#>  [49] 0.65691648 0.67235203 0.68750000 0.70234803 0.71688448 0.73109843
#>  [55] 0.74497968 0.75851875 0.77170688 0.78453603 0.79699888 0.80908883
#>  [61] 0.82080000 0.83212723 0.84306608 0.85361283 0.86376448 0.87351875
#>  [67] 0.88287408 0.89182963 0.90038528 0.90854163 0.91630000 0.92366243
#>  [73] 0.93063168 0.93721123 0.94340528 0.94921875 0.95465728 0.95972723
#>  [79] 0.96443568 0.96879043 0.97280000 0.97647363 0.97982128 0.98285363
#>  [85] 0.98558208 0.98801875 0.99017648 0.99206883 0.99371008 0.99511523
#>  [91] 0.99630000 0.99728083 0.99807488 0.99870003 0.99917488 0.99951875
#>  [97] 0.99975168 0.99989443 0.99996848 0.99999603 1.00000000
mazBETA(1.4,3,2)              #acquiring the moment about zero values
#> [1] 0.6
mazBETA(2,3,2)-mazBETA(1,3,2)^2 #acquiring the variance for a=3,b=2
#> [1] 0.04

#only the integer value of moments is taken here because moments cannot be decimal
mazBETA(1.9,5.5,6)
#> [1] 0.4782609